Les couleurs interférentielles

Vous avez sûrement déjà remarqué ces dégradés de couleurs vives et dansantes qu’on voit parfois sur de simples bulles de savon. Ces couleurs ne sont pas dues à un phénomène d’absorption sélective de la lumière par des colorants ou des pigments (voir notre page sur les couleurs chimiques). En effet, le savon utilisé pour faire ces bulles est incolore. Elles ne proviennent pas non plus, contrairement à ce qu’on lit parfois, d’une décomposition spectrale de la lumière comme dans un prisme. On va voir ici qu’elles sont dues à un phénomène d’interférences, lié à la nature ondulatoire de la lumière.
Sur quels types d'objets peut-on observer ces couleurs ?

Ces photos montrent différentes situations où des couleurs interférentielles peuvent être observées (voir notre page d’expériences pour en réaliser vous-mêmes). Quel est leur point commun ? Dans ces trois cas une lame mince est présente, sur ou dans l’objet considéré : à gauche une goutte d’huile se répand sur la surface d’une flaque d’eau en formant un film mince ; au centre la surface de l’urne en verre (musée des Romanités, Nîmes) est recouverte d’une fine couche, peut-être due à une oxydation ; à droite deux plaques de verre posées à plat l’une sur l’autre forment entre elles un mince interstice d’air.
Pour produire des couleurs contrastées, cette lame mince doit avoir une épaisseur de moins d’un micromètre (millième de millimètre). Pourquoi si mince ? Parce que le phénomène à l’origine de ces couleurs est intimement lié à la nature ondulatoire de la lumière, dont la longueur d’onde est justement de cet ordre de grandeur.
Pourquoi une lame mince fait-elle apparaître des couleurs ?
La lumière blanche qui nous éclaire habituellement (lumière du Soleil ou d’une lampe) est composée d’une superposition d’ondes de différentes longueurs d’onde. Chacune de ces ondes ou composante spectrale, vue séparément, correspond à une couleur dite « de l’arc-en-ciel ». Les longueurs d’ondes visibles à l’œil varient d’environ 0,4 à 0,7 micromètres, du côté violet au côté rouge du spectre. En cas de superposition, la couleur vue par l’œil dépend de la composition spectrale de la lumière selon le principe de la synthèse additive. Pour faire apparaître des couleurs à partir d’une lumière blanche, il faut retirer certaines composantes de son spectre. Nous allons expliquer comment la réflexion sur une lame mince rend cela possible.
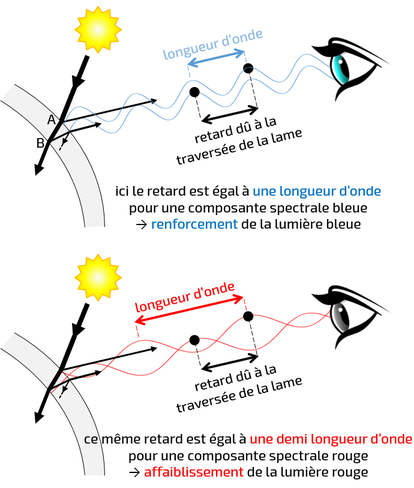
Considérons une des composantes spectrales de la lumière arrivant sur une lame mince. Elle rencontre sa première interface (point A sur le schéma) où elle est en partie réfléchie et en partie transmise. La partie transmise traverse la lame pour arriver sur sa seconde interface (point B) où elle est à nouveau en partie réfléchie et en partie transmise. Il n’y a donc pas une mais deux ondes réfléchies par une lame mince, à cause de ses deux interfaces.
La seconde onde a dû traverser deux fois l’épaisseur de la lame et elle se superpose donc à la première avec un certain retard, d’autant plus grand que la lame est épaisse. Si ce retard produit un décalage de l’onde dans l’espace égal à un nombre entier de fois sa longueur d’onde, les deux ondes réfléchies se superposent en vibrant en phase et donc se renforcent. On dit que les interférences sont constructives. Sinon leur superposition mène à une intensité lumineuse moindre, qui peut aller jusqu’à la suppression de l’onde réfléchie. On dit que les interférences sont destructives.
La lame mince réfléchit donc plus fortement certaines longueurs d’onde et en atténue d’autres. Le spectre de la lumière est ainsi modifié par réflexion sur la lame, ce qui crée une couleur. Mais à la différence de l’action d’un filtre à colorant, il n’y a pas ici d’absorption de la lumière : les longueurs d’ondes atténuées dans la lumière réfléchie par la lame mince sont renforcées dans la lumière qu’elle transmet, qui lui est donc complémentaire.
Remarque : si on tient compte des réflexions multiples à l’intérieur de la lame, qui à chaque aller-retour laissent sortir un peu de lumière à l’extérieur, il y a
en réalité un grand nombre d’ondes qui se superposent, avec des amplitudes de plus en plus faibles mais toujours le même décalage relatif dans l’espace. La prise en compte de l’ensemble de ces
ondes conduit à une sélection plus stricte des longueurs d’onde mais ne change pas les conclusions générales de ce qui est dit ici.
Les couleurs interférentielles ou teintes de Newton : un nuancier bien spécifique, qui nous informe sur l’épaisseur de la lame mince

Comme nous venons de le voir, c’est le retard dû à l’aller-retour dans l’épaisseur de la lame mince qui renforce certaines longueurs d’onde et en atténue d’autres.
Les couleurs interférentielles dépendent donc de l’épaisseur de la lame : elles se succèdent dans un dégradé de tonalités (jaune, orange, magenta, violet, bleu, cyan, vert, …) toujours
identique, qui se répète de moins en moins saturé lorsque l’épaisseur de la lame augmente. On peut le vérifier sur un film de savon vertical : par gravité l’épaisseur du film augmente de haut en bas, ce qui permet de visualiser toute la palette des couleurs
interférentielles dans l’ordre des épaisseurs croissantes (photo précédente, à gauche).
Ce nuancier, qu’on appelle « échelle des teintes de Newton », est différent de celui de l’arc-en-ciel (violet, bleu, vert, jaune, orange, rouge : photo précédente,
à droite), que l’on obtient par exemple en décomposant la lumière avec un prisme. En
particulier, il contient une couleur extra-spectrale, le magenta, qui ne peut être obtenue que par superposition de plusieurs longueurs d’onde et qui est donc absente de la liste des couleurs de
l’arc-en-ciel. Les teintes de Newton sont en revanche similaires aux couleurs de polarisation.

Pour vérifier que ces couleurs sont bien dues à la disparition de certaines longueurs d’onde dans le spectre de la lumière incidente, on a isolé ici, à l’aide d’un
logiciel permettant de séparer les 3 couches RVB d’une photo numérique, la composante rouge, verte ou bleue de la lumière (on aurait pu aussi observer l’image à travers un filtre coloré rouge, vert ou bleu).
Pour chaque composante, on voit une alternance de zones lumineuses et sombres, correspondant respectivement aux épaisseurs pour lesquelles les interférences sont constructives et destructives : à
mesure que le décalage entre les deux ondes réfléchies par la lame mince augmente, il devient égal à un nombre entier puis demi-entier de longueur d’onde.
Les positions des zones lumineuses et sombres ne sont pas les mêmes pour les trois composantes
rouge, verte et bleue de la lumière (elles ne correspondent pas à la même épaisseur de lame mince). L'addition de ces trois couches donne ainsi une grande variété de teintes.

Pour aller plus loin on peut analyser le spectre d’une couleur interférentielle à l’aide d’un appareil appelé spectromètre. On voit alors des maxima et des minima d’intensité qu’on appelle « cannelures » et qui correspondent respectivement aux interférences constructives et destructives. Leurs positions et leur nombre (dans la gamme spectrale visible) varient avec l’épaisseur de la lame mince. On montre ici des mesures réalisées dans trois zones d’un film de savon vertical.
- La zone A montre un spectre avec un seul minimum, dans la gamme vert-jaune. La lumière renvoyée par le film de savon est donc essentiellement un mélange additif de lumière bleue et rouge, que l’on perçoit magenta (l’intensité plus forte dans le rouge vient du fait qu’on a utilisé comme source une lampe à incandescence, dont l’émission augmente progressivement du bleu au rouge).
- Un peu plus bas, la zone B montre deux minima, dans la gamme des bleus et des rouges. La lumière renvoyée par le film est essentiellement dans la gamme des verts, ce qui explique qu’on perçoit une teinte verdâtre (un vert qui n’est pas pur spectralement).
- Beaucoup plus bas, la zone C montre un grand nombre de minima, donc aussi un grand nombre de maxima, aussi bien dans la gamme des bleus, verts et rouges. La lumière contient des composantes spectrales trop variées pour que notre œil perçoive une couleur interférentielle spécifique : si ses 3 types de cônes (voir notre page sur la vision des couleurs par l’œil) sont activés, il voit du « blanc », indépendamment de la position précise des maxima et des minima. En exploitant les positions de la dizaine de minima visibles sur le spectre, on peut déduire que l’épaisseur du film de savon dans la zone C est d’environ 2,2 micromètres.
On comprend ainsi comment l’épaisseur d’une lame joue sur la couleur interférentielle perçue. Si elle est assez faible pour qu’il n’y ait dans le spectre visible de la lumière réfléchie qu’un petit nombre de minima, leur position définit la couleur perçue. Plus la lame est épaisse, plus le nombre de minima dans le spectre visible est grand, ce qui produit une teinte de moins en moins saturée, jusqu’à ce qu’elle devienne insensible pour l’œil pour une épaisseur de quelques micromètres. Si vous voyez une couleur interférentielle sur une lame, vous pouvez donc très simplement en déduire que son épaisseur est micrométrique. C’est le cas du film de savon formant une bulle, ou d’une couche d’essence lorsqu’elle s’étend sur un sol mouillé. Dans ce dernier exemple, l’eau est nécessaire comme support car elle permet à l’essence, non miscible dans l’eau, de se répandre sur une grande surface, formant ainsi une très faible épaisseur.

Remarque : on peut se demander pourquoi ces couleurs ont été associées au nom de Newton, qui fut un fervent opposant à la théorie ondulatoire de la lumière. Newton les étudia au 17ème siècle, à l’aide d’un dispositif dit « des anneaux de Newton », formé d’une lame de verre à surface plane sur laquelle repose une lentille sphérique de très grand rayon de courbure, formant un mince interstice d’air d’épaisseur variable. Plus d’un siècle plus tard, c’est grâce à une analogie avec les ondes acoustiques et mécaniques que Thomas Young proposa l’interprétation ondulatoire aujourd’hui admise de ces couleurs. Dans un instrument de musique, il y a en effet un lien entre la fréquence de l’onde sonore émise, donc sa longueur d’onde, et la longueur de l’instrument (longueur d’un tuyau sonore ou d’une corde vibrante) : plus celui-ci est court, plus il fait résonner des longueurs d’onde courtes, donc des fréquences élevées, c’est-à-dire des notes aigües. Pour la lumière c’est la même chose : une lame plus mince fait « résonner » une longueur d’onde plus courte et donc donne une couleur interférentielle décalée vers le bleu. Cette interprétation a eu du mal à convaincre le monde scientifique de l’époque, à cause de l’influence encore grande des travaux de Newton. L’histoire retiendra pourtant le nom de « teintes de Newton » pour la palette des couleurs interférentielles, que Newton avait étudiées sans aboutir à une interprétation correcte du phénomène.
Pourquoi dit-t-on que ces couleurs sont « iridescentes » ?
Une particularité des couleurs interférentielles (c’est le cas aussi des couleurs de diffraction) est qu’elles sont susceptibles de varier selon l’angle sous lequel on les observe, ou celui sous lequel on les éclaire. Impossible d’obtenir cet effet avec une peinture classique à pigments !

Pour comprendre l’origine de ce phénomène, il faut reprendre plus précisément le schéma montrant le décalage entre les deux ondes qui vont interférer. Jusqu’ici on avait considéré implicitement un rayon lumineux arrivant à peu près perpendiculairement à la surface de la lame. Le décalage entre les deux ondes réfléchies est alors essentiellement dû à l’aller-retour fait par la seconde onde dans la lame (trajet A → B → A en pointillés longs sur le schéma de gauche). Si le rayon arrive en incidence oblique (schéma de droite) la seconde onde est davantage retardée car son trajet à l’intérieur de la lame (trajet A → B → C en pointillés longs) est plus long, mais la première onde prend aussi un retard, dû à un trajet supplémentaire à l’extérieur de la lame (trajet A → D en pointillés courts). Or il se trouve que le retard dû au trajet supplémentaire hors de la lame (A → D) est plus important que celui dû à l’augmentation du trajet dans la lame (différence entre le trajet A → B → C sur le schéma de droite et celui A → B → A sur celui de gauche). Le bilan est donc que l’inclinaison du rayon incident a pour effet de réduire le retard de la seconde onde par rapport à la première.
Puisque le décalage entre les deux ondes, responsable de la couleur interférentielle, diminue avec l’inclinaison du rayon lumineux sur la lame mince, la longueur d’onde sélectionnée diminue aussi. Si par exemple une lame mince donne une couleur interférentielle orange lorsqu’elle est observée de face, elle vire au jaune, puis au vert et au bleu à mesure qu’on l’observe en incidence plus rasante (l’ordre des couleurs correspond à celui que l’on observe quand l’épaisseur diminue, donc de bas en haut sur la photo du film de savon vertical montrée plus haut). On peut voir ces effets dans la nature, par exemple sur les élytres de certains coléoptères. On montre ici une cétoine, qu’on appelle « dorée » mais qui devient verte vue de côté.

Quelques applications des couleurs interférentielles

Les couleurs interférentielles donnent des effets très esthétiques, mais la sélection de longueurs d’onde par interférences a aussi de multiples applications. Comme application grand public, on peut citer les filtres antireflets : en déposant une couche mince à la surface d’un verre de lunettes, on peut éliminer par interférences la réflexion de la lumière pour certaines longueurs d’ondes, d’où un reflet plus faible mais coloré.
En laboratoire on s’en sert pour fabriquer des filtres qui sélectionnent très finement une gamme de longueur d’onde. On a dit plus haut qu’une simple lame mince ne permet pas de rendre la lumière pure spectralement, mais il est possible de le faire par exemple en associant plusieurs lames minces d’épaisseurs différentes. Un filtre interférentiel peut se reconnaître par le fait qu’il sélectionne une couleur variable selon son inclinaison.

En microélectronique, on détermine les épaisseurs de couches déposées sur des substrats de Silicium par l’analyse de leur couleur, à l’œil ou à l’aide d’un spectromètre. On montre ici une très belle image de M.J. Willis, qui a réalisé différentes épaisseurs de dépôts pour obtenir un bel effet coloré !

