Les couleurs de réfraction

Par une journée ensoleillée, vous êtes certainement déjà tombé(e) nez à nez avec un « spectre » projeté sur le sol ou sur un mur. Après avoir observé le magnifique dégradé de couleurs allant du rouge au violet, vous vous êtes demandé d’où ces couleurs pouvaient bien venir. Vous avez peut-être même poussé plus loin l’expérience en déplaçant votre main dans la lumière pour en chercher l’origine.
Dans cette page, nous allons présenter les phénomènes physiques et les conditions qui permettent d’observer ces dégradés de couleurs. Le cas particulier de l’arc-en-ciel est décrit sur une autre page.
Réfraction de la lumière et dispersion des couleurs

La lumière peut être décrite comme un ensemble de rayons qui en l’absence d’obstacles sont des lignes droites. Quand ces rayons changent de milieu, par exemple en passant de l’air dans l’eau, leur direction se modifie brusquement : on dit que la lumière est « réfractée » (une partie de la lumière est aussi réfléchie, on ne s’en préoccupera pas ici). C’est cette déviation qui explique que, quand on regarde un bâton partiellement immergé dans l’eau, il paraît brisé. Le phénomène de réfraction a de nombreuses applications pratiques : il intervient par exemple dans le fonctionnement des verres de lunettes qui permettent de corriger certains de nos défauts de vision.
Ce changement dans la direction des rayons lumineux obéit à une loi établie au 17ème siècle : la loi de Snell-Descartes. D’après cette loi, le rapport des sinus des angles d’incidence et de réfraction est égal au rapport de deux grandeurs caractéristiques des deux milieux traversés, appelées indices de réfraction, dont on ignorait à l’époque la signification. On comprit plus tard, avec la description ondulatoire de la lumière et notamment le principe de Huygens-Fresnel, que cet indice est inversement proportionnel à la vitesse de la lumière. Il est par définition égal à 1 dans le vide (qui sert donc de milieu de référence), 1,33 dans l’eau (ce qui signifie que la lumière s’y propage 1,33 fois moins vite que dans le vide) et 1,0003 dans l’air (où elle est très peu ralentie par rapport au vide). Des logiciels et des sites internet permettent de simuler, en utilisant la loi de Snell-Descartes, le trajet des rayons lumineux en présence de différents milieux dont les indices de réfraction sont connus, comme par exemple le site ostralo.net (nécessite d’activer Flash). Pour réaliser nos schémas nous avons utilisé le logiciel gratuit OptoGeo.
Mais une déviation des rayons lumineux ne suffit pas pour faire apparaître des couleurs à partir d’un rayon de lumière blanche : encore faut-il que cette déviation ne soit pas la même pour les différentes fréquences de vibration, correspondant aux couleurs « lumière » pures ou spectrales qui la composent.

Or il se trouve que dans la plupart des milieux matériels transparents que nous connaissons (par exemple le verre ou l’eau), la vitesse de propagation de la lumière varie de façon sensible avec sa fréquence de vibration. Les ondes lumineuses de plus faible fréquence (côté rouge du spectre visible) se propagent en effet un peu plus vite (l’indice de réfraction est plus faible), ce qui conduit, dans le cas d’une interface avec de l’air, à une déviation un peu plus faible que pour les ondes de fréquences élevées (côté violet du spectre). Les différentes composantes colorées de la lumière se séparent ainsi dans l’espace, car elles poursuivent leur chemin dans des directions différentes. On parle pour ce phénomène de « dispersion » et de milieu « dispersif ».
Les interfaces air/verre ou air/eau sont très courantes autour de nous, et pourtant l’effet de dispersion des couleurs n’est pas toujours clairement visible. C’est parce qu’il nécessite des conditions bien particulières, que nous allons décrire.
Pourquoi ne peut-on pas décomposer la lumière avec une simple vitre ?
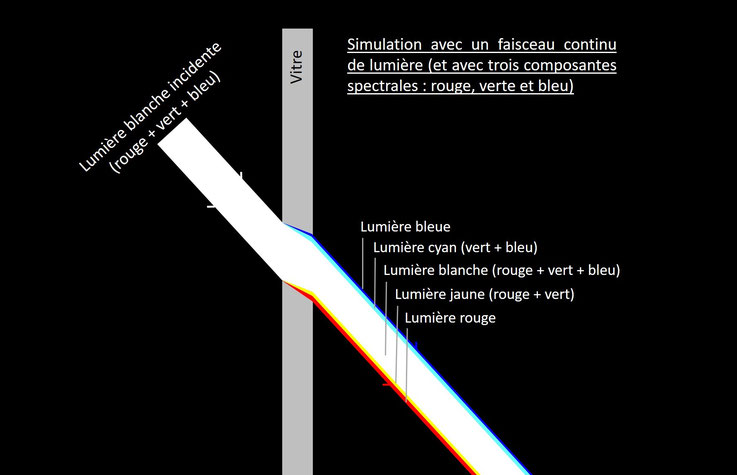
Le verre est un milieu dispersif, qui peut donc a priori décomposer la lumière blanche. Pourtant l’expérience quotidienne montre que ce phénomène n’est pas visible avec une simple vitre. Cela vient du fait que, si la lumière traverse les deux faces d'une couche de verre parallèles entre elles, la symétrie du problème est telle que la déviation d’un rayon lumineux à l’entrée dans le verre est exactement compensée par la déviation à la sortie. Des rayons rouge, vert et bleu issus d’un même rayon de lumière blanche ressortent donc parallèles entre eux, et très légèrement décalés (d’autant plus que la vitre est épaisse et l’incidence oblique). Quand le Soleil éclaire la surface d’une vitre, c’est tout un ensemble de rayons (qu’on appelle faisceau), en première approximation parallèles, qu’il faut prendre en compte. Les simulations ci-dessous illustrent le fait que, dans ces conditions, la réfraction ne permet pas de séparer les différentes couleurs spectrales présentes dans la lumière (sauf sur les bords du faisceau).

Une solution : le prisme
Pour éviter cette compensation entre les déviations angulaires à l’entrée et à la sortie du verre, il faut utiliser un objet dont les faces ne sont pas parallèles entre elles. C’est notamment le cas des prismes à base triangulaire, qui permirent à Isaac Newton en 1666 de comprendre que la lumière blanche n’est pas pure.
Si nous envoyons sur un tel prisme un rayon de lumière blanche, une première séparation angulaire des couleurs spectrales se produit à l’entrée dans le prisme (à peine visible sur notre schéma, construit avec les valeurs réelles des indices de réfraction d’un type de verre particulièrement dispersif). Celle-ci est amplifiée, et non compensée comme c’était le cas avec la vitre, par la deuxième réfraction, qui se produit à la sortie du prisme.

Bien sûr, il faut ici encore considérer l’effet de la largeur du faisceau (à moins d’utiliser une optique de focalisation). Même si les rayons sortants correspondant aux différentes composantes spectrales ne sont cette-fois pas parallèles entre eux, ils vont se recouvrir à proximité du prisme et se mélanger comme le feraient des lumières colorées.

Ce phénomène se voit très bien sur la photo ci-dessous, où un faisceau de lumière blanche issu d’une lampe halogène est envoyé sur un prisme en verre de type flint : le faisceau de lumière blanche à proximité immédiate du prisme devient nettement bordé de bleu et de rouge un peu plus loin, et enfin les couleurs du spectre apparaissent à une distance suffisamment grande du prisme.
Que se passe-t-il si on utilise le Soleil comme source de lumière ?
Vu de la Terre, le Soleil a un diamètre apparent d’environ un demi-degré. Cela implique que ses rayons ne nous parviennent pas parallèles entre eux mais sous un
angle qui peut varier sur un demi-degré, ce qui n’est pas forcément négligeable devant la faible dispersion angulaire obtenue par réfraction. Dans l’exemple du prisme en flint discuté
précédemment, qui est un milieu très dispersif, le schéma ci-dessous montre que la séparation angulaire induite par la dispersion entre les composantes spectrales rouge et bleu est seulement
quatre fois plus grande que celle induite par le diamètre apparent du Soleil. C’est juste suffisant pour séparer les composantes spectrales rouge et verte !
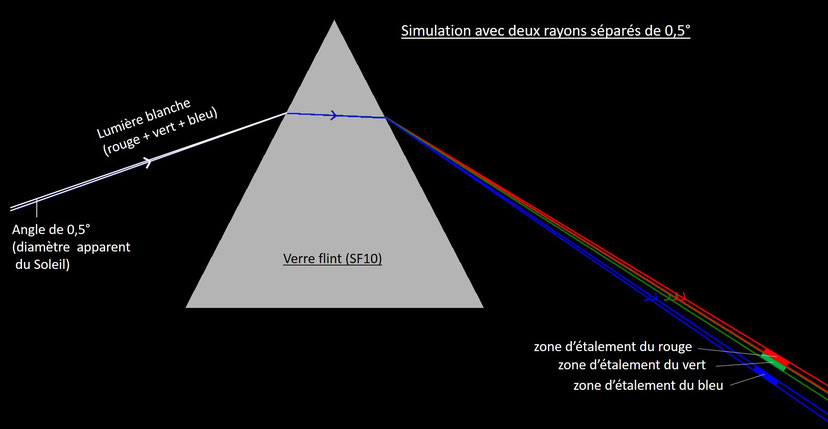
Pour autant les couleurs observées, même à grande distance du dispositif, ne sont pas « pures » (monochromatiques) puisque chaque composante spectrale s’étend sur une certaine largeur de faisceau : si la source émet un spectre continu, il y a recouvrement des composantes spectrales voisines, par exemple la zone d’étalement de la composante jaune (non représentée sur notre schéma) se mélange dans une certaine mesure avec celles des composantes rouge et verte. On pourrait s’en rendre compte en analysant finement la composition spectrale de ces couleurs à l'aide d'un spectromètre, ou éventuellement en les photographiant. Si l’on peut malgré tout voir à l’œil nu la succession des couleurs spectrales sur un écran, c’est grâce à notre système de vision des couleurs, qui repose sur seulement trois types de cônes : tant que le recouvrement entre les zones rouge et bleue du spectre reste limité, nous ne faisons pas de différence à l’œil avec un spectre de couleurs « lumière » pures. On peut d'ailleurs générer une succession de couleurs spectrales sur un écran d'ordinateur en mélangeant de façon ad-hoc des couleurs « lumière » rouge et verte puis verte et bleue.
Exemples de situations courantes où l’ on peut voir des couleurs de réfraction
L’arc-en-ciel est probablement la manifestation la plus spectaculaire des couleurs de réfraction. Sa description et sa compréhension font l’objet d’une page d’explications dédiée. Il est également possible de voir de belles décompositions colorées en passant à côté d’un morceau de verre biseauté ou en immergeant un miroir incliné dans l’eau (voir la page d’expériences : « décomposer la lumière du Soleil avec une bassine d’eau et un miroir »), comme le montrent les schémas et les photos ci-dessous.





