Les couleurs de diffraction

Certaines couleurs très particulières, qu'on appelle changeantes ou iridescentes, dépendent de la façon dont on regarde l'objet. Par exemple, l'ocelle de cette plume de paon (autour de la zone noire) peut être vue verte ou violette selon qu'on la regarde de face ou sous un angle rasant. Cet effet ne peut pas s'expliquer par un phénomène d'absorption de la lumière par des pigments. Il est dû à des phénomènes physiques liés à la nature ondulatoire de la lumière qu'on appelle la diffraction et les interférences. Ces phénomènes sont aussi à l'origine des couleurs changeantes qu'on peut observer sur la surface d'un CD. Nous allons voir comment ils induisent une séparation dans l'espace des couleurs lumières pures ou longueurs d'onde, mélangées dans la lumière blanche qui éclaire l'objet.
Les interférences

Commençons par expliquer le phénomène d’interférences en prenant l'exemple des vagues à la surface de l'eau. Une série de vagues issue d'un point source peut être représentée, à un instant donné et vue de dessus, par des cercles régulièrement espacés et centrés sur leur point d’émission. Représentons de cette façon deux séries de vagues identiques et régulières, émises à partir de deux points légèrement décalés, par exemple de gauche à droite. Nous constatons qu’il existe des lignes particulières le long desquelles une bosse d'une série de vagues coïncide avec un creux de l'autre série (lignes bleues sur le schéma) et d’autres le long desquelles deux bosses ou deux creux coïncident (lignes rouges sur le schéma). Lors de la propagation des vagues depuis leur point d’émission vers l'extérieur, les creux remplacent les bosses alternativement mais il se trouve que les lignes bleues et rouges sont toujours aux mêmes endroits.

En un point d'une ligne bleue, les deux séries de vagues ont des effets opposés : un creux de l'une coïncide avec une bosse de l'autre. Le résultat de la superposition est l’absence de vague : on parle d’interférences destructives.

En un point d'une ligne rouge, les deux séries de vagues ont des effets identiques : un creux de l'une coïncide avec un creux de l'autre (ou une bosse de l'une avec une bosse de l'autre). Le résultat de la superposition est une vague deux fois plus grande : on parle d’interférences constructives.
Une réalisation pratique de cette situation consiste à faire vibrer de façon synchrone deux boules à la surface de l'eau. Sur la photo ci-dessous extraite de cette vidéo, les lignes d'interférences destructives, caractérisées par l'absence de vagues, sont clairement visibles.
On peut plus facilement observer ces lignes en jetant dans l'eau deux petits cailloux, à
proximité l'un de l'autre :

Une façon très simple de visualiser et d'étudier ce phénomène en utilisant de la géométrie consiste à représenter la succession
de creux et de bosses par des lignes colorées régulièrement espacées, séparées par des zones blanches (cf. ci-dessous à gauche). Si nous superposons ainsi
deux ensembles identiques de vagues circulaires émises à partir de deux points différents, les directions dans lesquelles l’agitation de l’eau est maximale (lignes d'interférences constructives)
apparaissent claires, alors que les directions dans lesquelles elle est très atténuée ou nulle (lignes d'interférences destructives) sont celles où la coloration est maximale. L'apparition de cette modulation claire / sombre lorsqu'on superpose deux structures régulières s'appelle le moiré (qu'on observe parfois lorsque deux tissus à trame fine se
superposent). Il est alors facile de modifier l'espacement des sources ou la longueur d’onde (distance entre deux lignes successives) pour suivre
l'évolution de ces directions. Les images des ronds pour une source peuvent être téléchargées ici (format PDF) ou
là (format
PowerPoint) pour impression sur transparents ou manipulation sur ordinateur.


Cette animation montre un exemple d'observation facilement réalisable avec deux transparents qu'on déplace l'un par rapport à l'autre, ici dans la direction horizontale.
On peut voir que l’axe de symétrie du problème (ici l'axe vertical passant par le milieu des deux sources) correspond dans tous les cas à une direction d'interférences constructives. Quand l'espacement des deux sources est supérieur à la longueur d’onde, d’autres directions d’interférences constructives apparaissent de part et d'autre de l'axe de symétrie, d’autant plus resserrées et donc nombreuses que l'espacement des deux sources est grand par rapport à longueur d’onde. Cette animation permet également de visualiser cette tendance.
Quelque chose d’encore plus spectaculaire se produit quand les vagues émises par plus de deux sources régulièrement espacées le long d’une ligne interfèrent : plus le nombre de sources est grand, plus les vagues se concentrent dans les directions identifiées précédemment, et disparaissent partout ailleurs, au moins suffisamment loin des sources.


Cette animation montre ce qu'on observe en superposant de 1 à 7 séries de vagues circulaires, avec un écart constant (dans la direction horizontale) entre les points source : les zones blanches se concentrent sur des angles de plus en plus précis à mesure que le nombre de sources augmente.
Pour présenter ce phénomène d'interférences, nous avons choisi de commencer avec l'exemple des vagues
bien visibles à la surface de l'eau. Mais la même chose se produit avec n’importe quel type d’onde, donc en particulier avec la lumière. Dans ce cas, ce sont des vibrations électriques et magnétiques qui se propagent, à plusieurs centaines de milliers
de km/s et avec une longueur d’onde (pour la lumière visible) de l’ordre du micromètre (entre 0,4 et 0,7 micromètre, d'où les valeurs choisies pour les schémas
précédents). Supposons que nous puissions faire interférer plusieurs sources de lumière identiques et régulièrement espacées d’une distance comparable à la longueur d'onde, comme nous
l’avons fait précédemment avec nos modèles de vagues. La lumière se retrouverait alors concentrée dans des directions qui dépendent de la longueur d’onde
et nous aurions bien là une expérience
permettant de séparer les longueurs d'onde, donc les couleurs lumière pures, mélangées dans l'émission des sources. Cette expérience semble pour le moins difficile à faire puisqu'il faudrait disposer d'un grand nombre de sources lumineuses rigoureusement
identiques et suffisamment petites pour pouvoir être espacées d'une distance de l'ordre du micromètre ! Nous allons voir à présent comment le phénomène de
diffraction permet de faire cette expérience à partir d'une source de lumière unique et de taille
courante.
La diffraction

La diffraction est un phénomène peu intuitif, qui a pour conséquence que la lumière a tendance à
"s'éparpiller" lorsqu'elle traverse une ouverture de petite dimension, comparable à sa longueur d'onde. Si nous envoyons un faisceau de lumière parallèle sur une fente percée
dans une plaque opaque, nous nous attendons à retrouver sur un écran placé derrière, une bande lumineuse ayant la largeur de la fente. Mais si la largeur de la fente n'est pas trop grande devant
la longueur d'onde de la lumière, celle-ci part aussi sur les côtés et une zone beaucoup plus large de l’écran se retrouve éclairée. On dit que la lumière est diffractée par la fente. Ce phénomène, là encore lié à la nature ondulatoire de la lumière, se voit également très bien avec des vagues traversant une
ouverture.
En perçant dans une plaque opaque une fente d’une largeur inférieure au micromètre et en l’éclairant avec de la lumière, nous pouvons ainsi créer derrière la plaque une source d’ondes circulaires (vue de dessus) semblable aux schémas de vagues montrés précédemment. Si maintenant nous ne perçons pas une mais un grand nombre de fentes identiques régulièrement espacées, nous pouvons transformer une source lumineuse unique en autant de sources circulaires identiques qu’il y a de fentes. Nous pouvons ainsi réaliser l’expérience d’interférences décrite précédemment et séparer les ondes émises par la source dans des directions différentes selon leur longueur d'onde.
Nous vous invitons à observer sur les schémas suivants l'influence de l'espacement entre les fentes et de la longueur d'onde. En particulier, quand l'espacement entre les fentes augmente, les directions d'interférences constructives ont des angles plus petits donc sont plus nombreuses. Les directions d'interférences constructives à grande distance des fentes sont représentées par des tirets et identifiées par des numéros d'ordre, l'ordre 0 étant l'axe de symétrie des schémas.

Les réseaux de diffraction
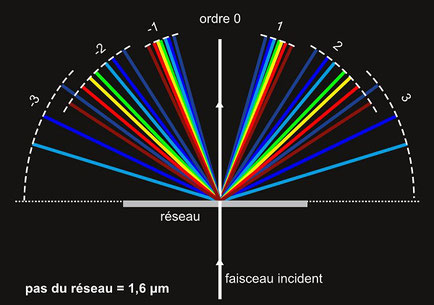
De tels objets, qu'on appelle des réseaux de diffraction, peuvent se fabriquer et il en existe même dans la nature ! Ils ne sont généralement pas constitués de fentes percées dans un milieu opaque, mais de "rayures" sur un support transparent, comme un film plastique ou une plaque de verre (les rayures diffractent la lumière comme des fentes). Si on envoie sur ce réseau un fin pinceau de lumière blanche composée de toutes les longueurs d’onde dans le domaine du visible, on verra apparaître sur un écran placé derrière, une ou plusieurs bandes aux couleurs de l’arc-en-ciel, de part et d’autre d'une tache blanche centrale. Chaque bande est identifiée par son numéro d'ordre, l'ordre 0 étant associé à la tache blanche centrale (la direction de l'ordre 0 étant identique pour chaque longueur d'onde, il n'y a pas de séparation des couleurs pour cet ordre). On peut voir sur le schéma que seules les bandes d'ordre 1 et -1 sont bien séparées des autres, et qu'un recouvrement se produit déjà entre les bandes d'ordres 2 et 3, et -2 et -3. Ce recouvrement se traduit par un mélange de couleurs lumières pures, semblable à ce que l'on obtient en mélangeant des lumières colorées sur un écran.
La photo ci-dessous montre un exemple de feuille réseau (disponible sur la boutique du site) et ce qu'on peut voir sur un écran placé derrière en l'éclairant avec un fin pinceau de lumière blanche. Les trois premiers ordres et leurs recouvrements sont clairement visibles de part et d'autre de la tache blanche centrale.
Les mêmes phénomènes d’interférences et de diffraction expliquent les reflets colorés à la surface d’un CD quand il est éclairé avec de la lumière blanche. La
surface d’un CD est en effet composée d’un long sillon, large d’environ 0,5 micromètre, qui s’enroule en spirale depuis le centre jusqu’à la périphérie du disque. La distance entre deux sillons
voisins est de 1,6 micromètre. Quand de la lumière est envoyée sur une telle structure, elle n’est pas simplement réfléchie comme sur la surface lisse d'un
miroir. Chaque sillon se comporte comme une fente dans une plaque opaque et diffracte (en réflexion cette fois) la lumière dans toutes les directions, car sa largeur est de l’ordre de la
longueur d’onde de la lumière. Les sillons étant régulièrement espacés, les lumières diffractées par les différents sillons interfèrent les unes avec les autres et conduisent à une séparation des
couleurs pures composant l'émission de la source, de part et d’autre d’une tache centrale blanche. Si une
surface importante du disque est éclairée, la figure est plus complexe : on retrouve dans les reflets
colorés la forme arrondie des sillons. Sur un DVD, les sillons sont plus serrés (0,74 micromètre entre deux sillons voisins) donc les directions des interférences constructives ont lieu pour des angles plus grands : seules les bandes d'ordre 1 ou -1 sont entièrement
visibles.



Voici donc comment la surface diffractante d'un CD peut produire des "arcs-en-ciel", en décomposant la lumière incidente blanche dans ses composantes pures. Mais attention : même si le résultat peut paraitre semblable, le phénomène physique en jeu dans les arcs colorés qu'on peut voir dans le ciel, les jours où la pluie et la lumière du soleil se mêlent, est très différent : dans ce dernier cas la séparation des couleurs dans l'espace (qu'on appelle dispersion) ne vient pas d'un phénomène de diffraction sur une surface finement striée, mais d'un phénomène de réfraction lors de la traversée des gouttes de pluie.



