>> Explications "vision"

Voir en relief

Notre perception du relief repose sur des informations de natures différentes. Il y a tout d’abord les contractions des muscles oculaires qui se produisent quand nous fixons un objet du regard. La déformation du cristallin permet de réaliser la mise au point à différentes distances, en focalisant les rayons lumineux issus d’un point de l’objet en un point de la rétine (c’est l’accommodation). Les mouvements des globes oculaires permettent quant à eux de déplacer les axes optiques des deux yeux pour faire converger leurs lignes de visée sur l’objet (c’est la convergence). Cette information est qualifiée de binoculaire car elle est relative aux deux yeux. Il y a ensuite tout un ensemble d’informations monoculaires présentes dans la scène que l’on regarde, comme l’existence de lignes de fuite, d’occlusions (on sait qu’un objet qui en cache partiellement un autre est placé devant), les tailles relatives des objets, ou les effets de parallaxe quand on est en mouvement (un objet plus proche semble se déplacer plus vite qu’un objet lointain). Même avec un seul œil, on peut donc percevoir (mais moins bien !) le relief.

Et si toutes ces informations nous sont très utiles dans notre vie quotidienne pour construire une représentation à trois dimensions de ce qui nous entoure, elles peuvent aussi être détournées pour nous « tromper ». Dans une Chambre d’Ames, on joue sur les indices monoculaires pour que deux personnes sensiblement de même taille paraissent de tailles très différentes. En revanche, dans le cas des anaglyphes que nous allons discuter ici, c’est l’indice binoculaire de convergence des lignes de visée qui est utilisé pour créer l’illusion du relief.

Principe général de la stéréoscopie

La stéréoscopie désigne l’ensemble des techniques permettant de percevoir du relief à partir d’une image plane, autrement dit d’avoir une vision « 3D » à partir d’une image 2D.

Pour comprendre comment cela est possible, nous vous invitons à réaliser une expérience toute simple. Placez-vous devant une fenêtre ou dehors et fixez un repère au loin. Puis portez devant vos yeux, d’abord relativement près, un stylo tenu à la verticale. Fermez un œil puis l’autre et regardez comment le stylo semble se déplacer par rapport au repère choisi. Vous constaterez qu’il se déplace de la gauche vers la droite quand on ferme successivement l’œil gauche puis l’œil droit, donc quand on passe de ce que voit l’œil droit à ce que voit l’œil gauche. Faites de même en éloignant le stylo de vous, le décalage observé est plus faible. Ce décalage est donc directement relié à la « profondeur » du stylo, c’est-à-dire sa distance à l’observateur.

C’est en utilisant ce décalage entre ce qui est vu par l’œil droit et par l’œil gauche qu’on arrive à donner une impression de relief à partir d’une image plane (imprimée sur une feuille ou affichée sur un écran d’ordinateur).

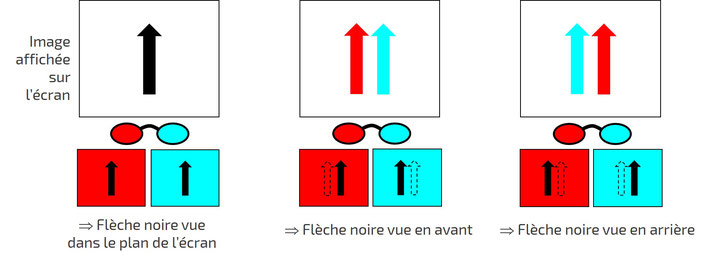
Cherchons pour en illustrer le principe à modifier la profondeur apparente d’un objet, ici une flèche blanche affichée à l’écran sur un fond noir. Dans la situation habituelle où nos deux yeux regardent un même point d’un objet (par exemple la pointe de la flèche), l’accommodation et la convergence des lignes de visée se font dans un même plan : celui de l’objet (schéma de gauche). Ces informations sont traitées par notre cerveau et nous « voyons » l’objet, ici à juste titre, dans le plan de l’écran.

Affichons à présent à l’écran une image avec deux flèches identiques, une à gauche qui n’est vue que par l’œil droit et une à droite qui n’est vue que par l’œil gauche (nous verrons plus loin comment cela peut être réalisé en pratique). Si chaque œil regarde la pointe de la flèche qui lui est visible, l’accommodation se fait toujours dans le plan de l’écran pour les deux yeux, mais les lignes de visée se croisent en avant de l’écran (schéma du milieu). C’est ce signal binoculaire de convergence qui, interprété par notre cerveau, nous conduit à « voir » une pointe de flèche située à l’avant de l’écran, au point de convergence des lignes de visée. Et si les deux flèches sont identiques, c’est une flèche toute entière qui nous apparaîtra en avant. Plus le décalage entre les deux flèches sur l’écran sera grand et plus nous « verrons » une flèche « proche » (dans une certaine limite car quand le décalage est trop grand, cela ne fonctionne plus ; sur nos schémas le décalage est exagéré pour faciliter les explications).

Si à l’inverse la flèche vue par l’œil droit est décalée à droite par rapport à celle vue par l’œil gauche, les lignes de visée se croisent à l’arrière de l’écran (schéma de droite). Ce signal binoculaire de convergence nous conduit cette fois à « voir » une flèche située à l’arrière de l’écran. En jouant ainsi sur le sens et l’amplitude du décalage entre les objets vus respectivement par chacun des deux yeux à l’écran, on peut modifier la profondeur apparente d’un objet.

Utilisation des couleurs rouge et cyan pour voir en relief : les anaglyphes

Mais comment faire en pratique pour que chacun des deux yeux ne voie pas la même chose quand ils regardent un même support plan, par exemple une image affichée sur un écran ? Une des techniques les plus anciennes, que nous allons décrire à présent, repose sur l’utilisation de lunettes dont les « verres » ont des couleurs complémentaires. L’image regardée qui donne l’illusion du relief est alors appelée un anaglyphe.

Cas d'une image restituée en "noir et blanc"

Appliquons les propriétés des couleurs rouge et cyan discutées précédemment et le principe général de la stéréoscopie à la construction d’anaglyphes. Nous commencerons par analyser le cas d’anaglyphes simples, constitués d’objets bien délimités et avec des couleurs homogènes (dessinés par exemple avec Paint), et qui permettent de voir des images restituées en noir et blanc. Les cas plus complexes d’images restituées en couleurs et à partir de photos seront discutés plus loin.

1er exemple : flèche blanche sur fond noir

Reprenons l’exemple précédent d’une unique flèche blanche sur fond noir affichée sur un écran. À travers des lunettes aux verres rouge/cyan, elle est vue rouge par l’œil gauche et cyan par l’œil droit. Notre système visuel localise la flèche dans le plan de l’écran, et par synthèse additive entre les signaux enregistrés par nos deux yeux, la flèche est vue blanche (moins lumineuse que si on la regarde directement sans lunettes).

Que se passe-t-il si on regarde avec ces mêmes lunettes une image composée de deux flèches identiques, l’une cyan décalée à gauche et l’autre rouge décalée à droite ? La flèche de gauche, cyan, est vue cyan par l’œil droit, noire par l’œil gauche pour lequel elle se confond avec le fond noir et n’est ainsi pas visible. De même la flèche de droite, rouge, est vue rouge par l’œil gauche, noire par l’œil droit pour lequel elle n’est donc pas visible. Ainsi, chaque œil ne voit qu’une seule des deux flèches, avec un décalage vers la droite pour l’œil gauche, comme dans l’exemple vu précédemment avec le stylo placé en avant du repère visé. Les lignes de visée des deux yeux se croisent devant l’écran, ce qui fait que nous « voyons » une flèche en avant de l’écran, blanche par synthèse additive. Attention : sur ce schéma et les suivants le décalage est exagéré pour faciliter les explications et ne permet pas de voir l’effet de relief avec des lunettes rouge/cyan.

Si on regarde à l’inverse une flèche rouge à gauche et une flèche cyan à droite, on verra une flèche blanche à l’arrière du plan de l’écran.

2ème exemple : flèche noire sur fond blanc

Dans le cas d’une flèche noire sur un fond blanc, la situation est inversée puisque c’est le fond de l’image qui émet ou renvoie de la lumière (blanche) et non la flèche elle-même.

Règle générale de construction

Des deux exemples précédents, nous pouvons déduire une règle simple permettant de construire l’anaglyphe d’un objet noir sur fond blanc ou blanc sur fond noir, pour des lunettes rouge/cyan. On commence par dupliquer l’image initiale noire et blanche en remplaçant le blanc dans un cas par du rouge, dans l’autre par du cyan. Pour faire apparaître un objet noir en avant sur un fond blanc, on décale l’image cyan/noire à gauche, celle rouge/noire à droite. Plus le décalage est grand et plus l’effet de relief sera important. Pour faire apparaître l’objet noir en arrière, il faut décaler les images en sens inverse. On fait ensuite la synthèse additive des deux images décalées, en appliquant les règles suivantes : rouge + cyan = blanc, rouge + noir = rouge, cyan + noir = cyan, noir + noir = noir. Enfin on rogne les bords, là où les images ne se recouvrent pas.

On peut appliquer ces règles pour construire l’anaglyphe d’une image plus complexe, composée de plusieurs objets situés à des profondeurs différentes, qu’on traitera donc par des décalages différents. Cela nécessite en toute rigueur de travailler avec une image de départ composée de différents « calques » superposés, chacun contenant des objets sensés être situés à une même profondeur, et d'appliquer aux composantes rouge et cyan de chaque calque des décalages différents, suivant la profondeur voulue. Il faudra aussi prendre soin de respecter la concordance des indices monoculaires, comme les tailles respectives des objets, les occlusions, etc.

Cas d'une image simple restituée en couleurs

Intéressons à présent au cas d’anaglyphes simples, toujours constitués d’objets bien délimités et homogènes, mais pouvant être colorés. La règle énoncée précédemment dans le cas d’images restitués en noir et blanc s’applique, mais le traitement des couleurs de l’objet et du fond rend les choses un peu plus complexes. On commence par séparer les composantes rouge et cyan de l’image de départ. Si l’image a été faite avec un logiciel de dessin comme Paint, il suffit de sélectionner chaque élément (le fond de l’image, l’objet) et de modifier son code RVB de la façon suivante : en mettant R à zéro, on élimine la composante rouge et on obtient la composante cyan ; en mettant V et B à zéro, on élimine les composantes verte et bleue et on obtient la composante rouge. Pour un carré jaune (code RVB = 255 ; 255; 0) sur fond noir (code RVB = 0 ; 0 ; 0), la composante cyan sera un carré vert (code RVB = 0 ; 255 ; 0) sur fond noir et la composante rouge un carré rouge (code RVB = 255 ; 0 ; 0) sur fond noir. On obtient ensuite l’anaglyphe en faisant la synthèse additive des deux composantes cyan et rouge décalées. Pour cela, on identifie les zones de recouvrement des objets des images décalées, puis on fait « à la main » la somme des codes RVB de ces différentes zones. Dans notre exemple, là où le carré vert et le fond noir se superposent, on aura du vert ; là où le carré vert et le carré rouge se superposent, on aura du jaune, enfin là où le carré rouge et le fond noir se superposent, on aura du rouge.

Le rendu des couleurs avec un anaglyphe reste cependant limité : pour des lunettes rouge/cyan, il n’est par exemple pas possible de modifier la profondeur d’un carré rouge ou d’un carré cyan, car un tel carré ne sera vu que par un œil. Suivant les couleurs que l’on souhaite restituer, il peut donc être préférable de s’orienter vers un autre couple de couleurs complémentaires. L’utilisation de couleurs non complémentaires est également possible : il suffit de choisir un couple de couleurs tel qu’aucune composante spectrale (idéalement) ne peut traverser à la fois un verre et l’autre, ce qui est le cas par exemple du couple rouge/vert (une lumière verte ne traverse pas un filtre rouge et inversement). Mais cela réduira plus encore le champ des couleurs possibles : par exemple, avec des verres colorés rouge et vert, un objet de couleur rouge ou verte ne sera pas vu en relief, mais ce sera le cas également pour un objet bleu, qui sera vu noir par les deux yeux.

Anaglyphes réalisés à partir de photos numériques couleurs

Comment réalise-t-on des anaglyphes plus complexes permettant de visualiser en relief des scènes réelles (paysage ou autre) avec des lunettes rouge/cyan ? La technique la plus précise consiste à prendre deux photographies en couleurs d’une même scène, avec deux angles de vue légèrement différents. On pourra utiliser deux appareils photos écartés horizontalement, ou si le sujet photographié est fixe, un seul appareil photo que l’on déplace entre deux prises de vue. Ces photos sont ensuite « traitées » à l’aide d’un logiciel spécialisé dans la fabrication d’anaglyphes (on trouve de nombreux exemples sur internet) de la manière suivante. On superpose les deux photos afin de corriger les éventuelles distorsions, défauts d’alignement et autres. Les différents éléments qui les composent se retrouvent d’autant plus décalés qu’ils sont proches de l’observateur. On fait glisser horizontalement les deux images l’une sur l’autre afin de choisir le plan où les éléments seront superposés (ils seront ensuite vus dans le plan de l’anaglyphe). On conserve la composante rouge de l’image de gauche, et la composante cyan de l’image de droite. On obtient finalement l’anaglyphe en faisant la synthèse additive de ces deux composantes et en rognant les bords. En pratique, pour un résultat optimum, d’autres opérations sont nécessaires : modification des couleurs de l’image en fonction des filtres utilisés pour les lunettes, du rendu des couleurs sur l’écran, etc.

On trouve de très nombreux exemples de ces anaglyphes sur internet, notamment sur le site du Stéréo-Club Français. L'effet de relief se voit très bien sur l’exemple ci-dessous. Les poteaux verticaux de la barrière en bois ne montrent pas de décalage horizontal entre les images rouge et cyan pour le poteau le plus à gauche de l’image, plan choisi pour la convergence dans le plan de l’anaglyphe. Un décalage de plus en plus grand est visible pour les poteaux partant vers la droite, dont la composante cyan est décalée à gauche. Ils seront donc interprétés de plus en plus en profondeur.

Le traitement des couleurs se voit très bien sur cette autre image, toujours extraite d’un des albums du Stéréo-Club Français. Le ballon jaune est décomposé en une composante rouge et une composante verte, le ballon magenta en une composante rouge et une composante bleue. On constate que le rendu des couleurs est limité : à travers les lunettes rouge/cyan il y a peu de différences entre les ballons vert et jaune d’une part, et les ballons cyan et magenta d’autre part. On a donc gagné du relief en perdant (partiellement) la couleur.

Il est aussi possible de réaliser des anaglyphes à partir d’une seule photo. Dans ce cas, la photo est décomposée en ses composantes rouge et cyan. Puis on définit « à la main » dans un logiciel de traitement d’images une échelle de profondeur pour les différents plans. Le logiciel décale ensuite les images rouge et cyan en fonction, ce qui donne la perception de relief. Le rendu est bien sûr de moins bonne qualité.

Des anaglyphes au cinéma « 3D » d'aujourd'hui

Si les anaglyphes sont toujours utilisés aujourd’hui, d’autres techniques plus performantes ont été développées, notamment pour le cinéma dit « 3D » (il ne s’agit pas de « vrai 3D » car le procédé ne fournit un relief que depuis un seul point de vue, contrairement à l’holographie). Le procédé actuellement le plus répandu consiste à utiliser non pas la composition spectrale (la couleur) de la lumière, mais une autre propriété appelée la polarisation. Deux images dont les polarisations tournent en sens inverse (circulaire gauche et circulaire droite) sont projetées sur l’écran, et grâce à des lunettes dont les verres sont munis de filtres polarisants ad-hoc, chaque œil du spectateur ne voit qu’une seule des deux images. Comme pour les anaglyphes, la stéréoscopie génère l’impression de relief. L’avantage est que, nos yeux n’étant pas sensibles à la polarisation de la lumière, l’image perçue par chaque œil n’est pas modifiée (pour l’œil) par les filtres polarisants. Il n’y a en particulier pas de perte d’information colorée comme on vient de le constater dans l’exemple précédent avec les filtres de couleurs complémentaires.

La stéréoscopie aussi dans les appareils photo de nos smartphones ?

>> Explications "vision"